সংখ্যা পদ্ধতিঃ
যে পদ্ধতিতে সংখ্যা গণনা করা হয় বা প্রকাশ করা হয়, তাকে সংখ্যা পদ্ধতি (Number systems) বলে। এসকল সংখ্যাকে বিভিন্ন গাণিতিক প্রক্রিয়ার মাধ্যমে প্রয়োজনীয় গণনার কাজ করা হয়। সংখ্যা পদ্ধতি হলো এমন একটি পদ্ধতি যার মাধ্যমে আমরা সংখ্যাগুলি প্রকাশ এবং ব্যবহার করি। গণিত, কম্পিউটার বিজ্ঞান এবং দৈনন্দিন জীবনের বিভিন্ন ক্ষেত্রে সংখ্যা পদ্ধতি গুরুত্বপূর্ণ ভূমিকা পালন করে।
যে পদ্ধতিতে বিভিন্ন সংখ্যা লিখে প্রকাশ করা যায় এবং উক্ত সংখ্যাগুলোর উপর বিভিন্ন অপারেশন প্রয়োগ, যথা- যোগ, বিয়োগ, ভাগ, গুণ, এবং শতকরায় রুপান্তর করে হিসেব নিকেশ সম্পাদান করা যায়, তাকে সংখ্যা পদ্ধতি বলে।
সংখ্যা তৈরির ক্ষুদ্রতম একক হচ্ছে অঙ্ক, যেমন ১, ২, ৩। দৈনিন্দিন কাজে আমরা সাধারণত দশমিক সংখ্যা ব্যহার করি, কিন্তু বর্তমানে কিছু মেশিনভিত্তিক সংখ্যা ব্যবহার করা হয়। যথা- বাইনারি, অক্টাল, এবং হেক্সাডেসিমল।
সংখ্যা পদ্ধতির প্রকারভেদঃ
সংখ্যা পদ্ধতির প্রধান চারটি ধরন হলো:
1. দশমিক সংখ্যা পদ্ধতি (Decimal Number System)**
2. বাইনারি সংখ্যা পদ্ধতি (Binary Number System)**
3. অক্টাল সংখ্যা পদ্ধতি (Octal Number System)**
4. হেক্সাডেসিমাল সংখ্যা পদ্ধতি (Hexadecimal Number System)**
১. দশমিক সংখ্যা পদ্ধতি (Decimal Number System):
দশমিক সংখ্যা পদ্ধতি হল সবচেয়ে প্রচলিত এবং প্রাচীন সংখ্যা পদ্ধতি যা আমরা দৈনন্দিন জীবনে ব্যবহার করি। এই সংখ্যা পদ্ধতি বেস-১০ পদ্ধতি হিসেবে পরিচিত, কারণ এতে ১০টি মৌলিক সংখ্যা (০ থেকে ৯ পর্যন্ত) ব্যবহার করা হয়।

দশমিক সংখ্যা পদ্ধতির গঠন:
দশমিক সংখ্যা পদ্ধতিতে প্রতিটি সংখ্যার মান তার অবস্থান (position) বা স্থানীয় মান (place value) দ্বারা নির্ধারিত হয়। প্রতিটি অবস্থানের মান ১০-এর ঘাত (power) হিসেবে বৃদ্ধি পায়। উদাহরণস্বরূপ, সংখ্যা 3456 কে বিশ্লেষণ করলে:
এখানে,
-
৬ এর স্থানীয় মান (place value) হল ৬,
-
৫ এর স্থানীয় মান হল ৫০,
-
৪ এর স্থানীয় মান হল ৪০০,
-
৩ এর স্থানীয় মান হল ৩০০০।
২. বাইনারি সংখ্যা পদ্ধতি (Binary Number System):
বাইনারি সংখ্যা পদ্ধতি একটি মৌলিক সংখ্যা পদ্ধতি । যা ০ এবং ১ এর সমন্বয়ে গঠিত একটি সংখ্যা পদ্ধতি। বাইনারি শব্দটি ল্যাটিন শব্দ “বিনারি” থেকে উদ্ভূত হয়েছে, যার অর্থ “দুই দ্বারা গঠিত”। এই সংখ্যা পদ্ধতিতে শুধুমাত্র দুটি ডিজিট রয়েছে, ০ এবং ১। বাইনারি সংখ্যা পদ্ধতি ব্যবহার করে জটিল গাণিতিক ক্রিয়াকলাপ এবং তথ্য প্রক্রিয়াকরণ সম্ভব হয়।
এটি ‘বেস-২’ সংখ্যা পদ্ধতি নামেও পরিচিত। বাইনারি সংখ্যা পদ্ধতি অত্যন্ত গুরুত্বপূর্ণ কারণ এটি কম্পিউটার এবং অন্যান্য ডিজিটাল সিস্টেমের জন্য মূল ভিত্তি হিসেবে কাজ করে। কম্পিউটার শুধুমাত্র দুটি অবস্থা বুঝতে পারে: On(১) এবং Off(০)। এই দুটি অবস্থার সাহায্যে সমস্ত তথ্য বাইনারি আকারে উপস্থাপন করা হয়।
বাইনারি সংখ্যা পদ্ধতি দিয়ে বিভিন্ন ধরনের তথ্য সংরক্ষণ করা যায় যেমন টেক্সট, ছবি, ভিডিও ইত্যাদি। প্রতিটি ডেটা একটি নির্দিষ্ট বিন্যাসে বাইনারি সংখ্যায় রূপান্তরিত হয় এবং তারপর কম্পিউটারের মেমোরিতে সংরক্ষিত হয়। উদাহরণস্বরূপ, “A” অক্ষরটি ASCII কোড অনুযায়ী বাইনারি সংখ্যায় “01000001” দ্বারা প্রতিনিধিত্ব করা হয়।

বিশ্লেষণ:
বাইনারি সংখ্যা পদ্ধতিতে সংখ্যাগুলির অবস্থান অনুযায়ী ২-এর ঘাত ব্যবহার করে দশমিক সংখ্যায় রূপান্তর করা হয়। এখানে আমরা সংখ্যা 1101-কে বিশ্লেষণ করব এবং দেখব কিভাবে এটি দশমিক সংখ্যায় রূপান্তরিত হয়।
পদক্ষেপ ১: বাইনারি সংখ্যার প্রতিটি ডিজিট নির্ধারণ
বাইনারি সংখ্যা 1101-এ প্রতিটি ডিজিটের অবস্থান এবং মান:
-
সর্বডানের (ডান থেকে প্রথম) সংখ্যা ১
-
দ্বিতীয় সংখ্যা ০
-
তৃতীয় সংখ্যা ১
-
চতুর্থ সংখ্যা ১
পদক্ষেপ ২: প্রতিটি ডিজিটকে ২-এর ঘাত হিসেবে প্রকাশ
প্রতিটি ডিজিটকে তার অবস্থান অনুযায়ী ২-এর ঘাত হিসেবে লিখতে হবে। ডান দিক থেকে বাম দিকে শুরু করে প্রতিটি সংখ্যা ২-এর ঘাতের সাথে গুণ করতে হবে।
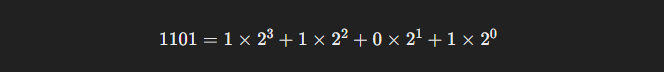
পদক্ষেপ ৩: প্রতিটি ডিজিটের গুণফল নির্ধারণ
প্রতিটি ডিজিটকে তার ২-এর ঘাতের মান দিয়ে গুণ করি:
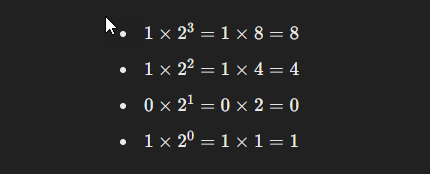
পদক্ষেপ ৫: গুণফলগুলো যোগ করা
এখন প্রতিটি ডিজিটের গুণফলগুলো যোগ করি: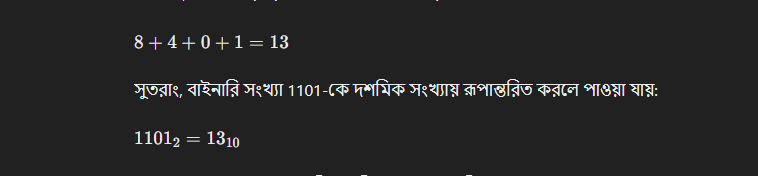
এভাবে, সংখ্যা 1101 (বাইনারি) দশমিক সংখ্যা পদ্ধতিতে 13 হয়।
৩. অক্টাল সংখ্যা পদ্ধতি (Octal Number System)
অক্টাল সংখ্যা পদ্ধতি হল বেস-৮ পদ্ধতি যেখানে ০ থেকে ৭ পর্যন্ত মোট আটটি সংখ্যা ব্যবহৃত হয়। এটি কম্পিউটার সিস্টেমে কিছু নির্দিষ্ট ক্ষেত্রে ব্যবহৃত হয়, বিশেষত যখন বাইনারি সংখ্যাগুলি সংক্ষিপ্ত আকারে উপস্থাপন করতে হয়।
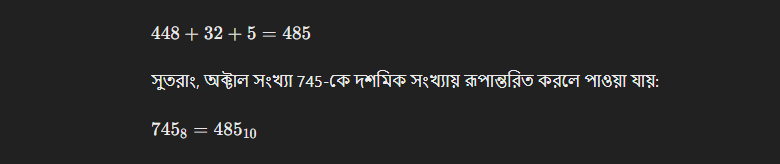
উদাহরণ: সংখ্যা 745 কে অক্টাল সংখ্যা পদ্ধতিতে বিশ্লেষণ করা যায়:
বিশ্লেষণ:
অক্টাল সংখ্যা পদ্ধতিতে সংখ্যাগুলির অবস্থান অনুযায়ী ৮-এর ঘাত ব্যবহার করে দশমিক সংখ্যায় রূপান্তর করা হয়। এখানে আমরা সংখ্যা 745-কে বিশ্লেষণ করব এবং দেখব কিভাবে এটি দশমিক সংখ্যায় রূপান্তরিত হয়।
পদক্ষেপ ১: অক্টাল সংখ্যার প্রতিটি ডিজিট নির্ধারণ
অক্টাল সংখ্যা 745-এ প্রতিটি ডিজিটের অবস্থান এবং মান:
-
সর্বডানের (ডান থেকে প্রথম) সংখ্যা ৫
-
দ্বিতীয় সংখ্যা ৪
-
তৃতীয় সংখ্যা ৭
পদক্ষেপ ২: প্রতিটি ডিজিটকে ৮-এর ঘাত হিসেবে প্রকাশ
প্রতিটি ডিজিটকে তার অবস্থান অনুযায়ী ৮-এর ঘাত হিসেবে লিখতে হবে। ডান দিক থেকে বাম দিকে শুরু করে প্রতিটি সংখ্যা ৮-এর ঘাতের সাথে গুণ করতে হবে।
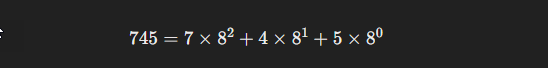
পদক্ষেপ ৩: প্রতিটি ডিজিটের গুণফল নির্ধারণ
প্রতিটি ডিজিটকে তার ৮-এর ঘাতের মান দিয়ে গুণ করি:
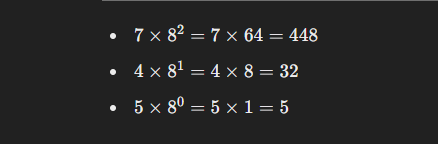
পদক্ষেপ ৪: গুণফলগুলো যোগ করা
এখন প্রতিটি ডিজিটের গুণফলগুলো যোগ করি:


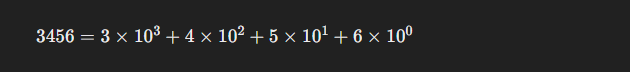




need more details